辉忆年
0%

树形dp习题

发表于 更新于 分类于 Valine：
题目 链接
hdu 2196 Computer http://acm.hdu.edu.cn/showproblem.php?pid=2196
poj 1463 Strategic game http://poj.org/problem?id=1463
P3574 [POI2014]FAR-FarmCraft https://www.luogu.com.cn/problem/P3574
…… ……

hdu 2196 Computer

Problem Description

A school bought the first computer some time ago(so this computer’s id is 1). During the recent years the school bought N-1 new computers. Each new computer was connected to one of settled earlier. Managers of school are anxious about slow functioning of the net and want to know the maximum distance Si for which i-th computer needs to send signal (i.e. length of cable to the most distant computer). You need to provide this information.
img

Hint: the example input is corresponding to this graph. And from the graph, you can see that the computer 4 is farthest one from 1, so S1 = 3. Computer 4 and 5 are the farthest ones from 2, so S2 = 2. Computer 5 is the farthest one from 3, so S3 = 3. we also get S4 = 4, S5 = 4.

Input

Input file contains multiple test cases.In each case there is natural number N (N<=10000) in the first line, followed by (N-1) lines with descriptions of computers. i-th line contains two natural numbers - number of computer, to which i-th computer is connected and length of cable used for connection. Total length of cable does not exceed 10^9. Numbers in lines of input are separated by a space.

Output

For each case output N lines. i-th line must contain number Si for i-th computer (1<=i<=N).

Sample Input

1
2
3
4
5
5
1 1
2 1
3 1
1 1

Sample Output

1
2
3
4
5
3
2
3
4
4

Solution 1：树的直径

找到树直径的两个端点A，B。求每个节点到A，B的距离。结果为max(disA, disB)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <bits/stdc++.h>

#define db1(x) cout << #x << " = " << x << endl
#define db2(x, y) cout << #x << " = " << x << ", " << #y << " = " << y << endl
#define paging cout << "------------------" << endl
#define all(x) x.begin(), x.end()
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 1e4 + 10;
int n;
vector<pii> adj[N];
int d[N];
int len;
int pos;
int dis[N][2];
void dfs(int u, int p, int cnt) {
    if(len < cnt) {
        len = cnt;
        pos = u;
    }
    for (pii node : adj[u]) if(node.first != p) {
        int v = node.first;
        int c = node.second;
        dfs(v, u, cnt + c);
    }
}
void dfs1(int u, int p, int id) {
    for (pii node : adj[u]) if(node.first != p) {
        int v = node.first;
        int c = node.second;
        dis[v][id] = dis[u][id] + c;
        dfs1(v, u, id);
    }
}
void sol() {
    while(~scanf("%d", &n)) {
        for (int i = 1; i <= n; ++ i) adj[i].clear(), d[i] = 0;
        for (int i = 2; i <= n; ++ i) {
            int v, c; scanf("%d%d", &v, &c);
            adj[i].push_back({v, c});
            adj[v].push_back({i, c});
        }
        memset(dis, 0, sizeof(dis));
        len = pos = 0;
        dfs(1, 1, 0);
        dfs1(pos, pos, 0);
        len = 0;
        dfs(pos, pos, 0);
        dfs1(pos, pos, 1);
        for (int i = 1; i <= n; ++ i) printf("%d\n", max(dis[i][0], dis[i][1]));
    }
}
int main() {
//    int _; scanf("%d", &_); while(_ --)
    sol();
    return 0;
}

Solution 2：树形dp

d[i, 0]：i往下走的最大距离

d[i, 1]：i往下走的次大距离

d[i, 2]：i往上走的最大距离

d[i, 0]和d[i, 1]可以同过一个dfs直接求出。

d[i, 2]分两种情况。假设现在求d[j, 2]。i是j的父节点。

若d[i, 0]的路径经过j。那么d[j, 2] = cost[i, j] + max(d[j, 2], d[j, 1] )。

若不经过，d[j, 2] = cost[i, j] + max(d[j, 2], d[j, 0] )。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <bits/stdc++.h>

#define db1(x) cout << #x << " = " << x << endl
#define db2(x, y) cout << #x << " = " << x << ", " << #y << " = " << y << endl
#define paging cout << "------------------" << endl
#define all(x) x.begin(), x.end()
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 1e4 + 10;
int n;
vector<pii> adj[N];
int d[N][3];
int go[N];
void dfs1(int u = 1, int p = 1) { // get d[][0] and d[][1]
    for (pii node : adj[u]) if(node.first != p) {
        int v = node.first, c = node.second;
        dfs1(v, u);
        int val = d[v][0] + c;
        if(val >= d[u][0]) {
            go[u] = v;
            d[u][1] = d[u][0];
            d[u][0] = val;
        } else if(val > d[u][1]) d[u][1] = val;
    }
}
void dfs2(int u = 1, int p = 1) { // get d[][2]
    for (pii node : adj[u]) if(node.first != p) {
        int v = node.first, c = node.second;
        if(go[u] == v) d[v][2] = max(d[u][2], d[u][1]) + c;
        else d[v][2] = max(d[u][2], d[u][0]) + c;
        dfs2(v, u);
    }
}
void sol() {
    while(~scanf("%d", &n)) {
        for (int i = 1; i <= n; ++i) adj[i].clear();
        for (int i = 2; i <= n; ++i) {
            int v,c; scanf("%d%d", &v, &c);
            adj[i].push_back({v, c});
            adj[v].push_back({i, c});
        }
        memset(d, 0, sizeof(d));
        memset(go, 0, sizeof(go));
        dfs1();
        dfs2();
        for (int i = 1; i <= n; ++ i) printf("%d\n", max(d[i][0], d[i][2]));
    }
}
int main() {
    sol();
    return 0;
}

poj 1463 Strategic game

Description

Bob enjoys playing computer games, especially strategic games, but sometimes he cannot find the solution fast enough and then he is very sad. Now he has the following problem. He must defend a medieval city, the roads of which form a tree. He has to put the minimum number of soldiers on the nodes so that they can observe all the edges. Can you help him?

Your program should find the minimum number of soldiers that Bob has to put for a given tree.

For example for the tree: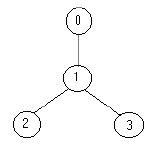
img
the solution is one soldier ( at the node 1).

Input

The input contains several data sets in text format. Each data set represents a tree with the following description:

  • the number of nodes
  • the description of each node in the following format
    node_identifier:(number_of_roads) node_identifier1 node_identifier2 … node_identifiernumber_of_roads
    or
    node_identifier:(0)

The node identifiers are integer numbers between 0 and n-1, for n nodes (0 < n <= 1500);the number_of_roads in each line of input will no more than 10. Every edge appears only once in the input data.

Output

The output should be printed on the standard output. For each given input data set, print one integer number in a single line that gives the result (the minimum number of soldiers). An example is given in the following:

Sample Input

1
2
3
4
5
6
7
8
9
10
11
4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)

Sample Output

1
2
1
2

Solution: 树形dp

从下往上递推。每个节点有两个状态。

d[i, 0]：以i为根节点，在i节点不放人的情况，所需的最小人数。= sum(d[son, 1])

d[i, 1]：以i为根节点，在i节点放人的情况，所需的最小人数。 = 1 + sum (min(d[son, 0], d[son, 1] ) )

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
//#include <bits/stdc++.h>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>

#define db1(x) cout << #x << " = " << x << endl
#define db2(x, y) cout << #x << " = " << x << ", " << #y << " = " << y << endl
#define paging cout << "------------------" << endl
#define all(x) x.begin(), x.end()
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 1e4 + 10;
int n;
vector<int> adj[N];
int d[N][2];
void dfs(int u = 1, int p = 1) {
    int sum0, sum1;
    sum0 = 0; sum1 = 1;
    for (int i = 0; i < adj[u].size(); ++ i) if(adj[u][i] != p) {
        int v = adj[u][i];
        dfs(v, u);
        sum0 += d[v][1];
        sum1 += min(d[v][0], d[v][1]);
    }
    d[u][1] = sum1;
    d[u][0] = sum0;
}
void sol() {
    while(~scanf("%d", &n)) {
        for (int i = 0; i < n; ++ i) adj[i].clear();
        for (int i = 0; i < n; ++ i) {
            int u, len; scanf("%d:(%d)", &u, &len);
            for (int j =0 ; j <len; ++j) {
                int v; scanf("%d", &v);
                adj[u].push_back(v);
                adj[v].push_back(u);
            }
        }
        dfs();
        printf("%d\n", min(d[1][0], d[1][1]));
    }
}
int main() {
    sol();
    return 0;
}

P3574 [POI2014]FAR-FarmCraft

题目描述

In a village called Byteville, there are n houses connected with n-1 roads.

For each pair of houses, there is a unique way to get from one to another.

The houses are numbered from 1 to n.

The house no. 1 belongs to the village administrator Byteasar.

As part of enabling modern technologies for rural areas framework, n computers have been delivered to Byteasar’s house.

Every house is to be supplied with a computer, and it is Byteasar’s task to distribute them.

The citizens of Byteville have already agreed to play the most recent version of FarmCraft (the game) as soon as they have their computers.

Byteasar has loaded all the computers on his pickup truck and is about to set out to deliver the goods.

He has just the right amount of gasoline to drive each road twice.

In each house, Byteasar leaves one computer, and immediately continues on his route.

In each house, as soon as house dwellers get their computer, they turn it on and install FarmCraft.

The time it takes to install and set up the game very much depends on one’s tech savviness, which is fortunately known for each household.

After he delivers all the computers, Byteasar will come back to his house and install the game on his computer.

The travel time along each road linking two houses is exactly 1 minute, and (due to citizens’ eagerness to play) the time to unload a computer is negligible.

Help Byteasar in determining a delivery order that allows all Byteville’s citizens (including Byteasar) to start playing together as soon as possible.

In other words, find an order that minimizes the time when everyone has FarmCraft installed.

输入格式

The first line of the standard input contains a single integer n(2 <= n <= 500 000) that gives the number of houses in Byteville.

The second line contains n integers c1, c2 …… cn, (1 <= ci <= 109),separated by single spaces; ci is the installation time (in minutes) for the dwellers of house no. i.

The next n-1 lines specify the roads linking the houses.

Each such line contains two positive integers a and b (1<= a < b <= n), separated by a single space.These indicate that there is a direct road between the houses no. a and b.

输出格式

The first and only line of the standard output should contain a single integer:

the (minimum) number of minutes after which all citizens will be able to play FarmCraft together.

输入样例

1
2
3
4
5
6
7
6
1 8 9 6 3 2
1 3
2 3
3 4
4 5
4 6

输出样例

1
11

Solution：树形dp+贪心

从root开始遍历，最后在回来。遍历耗时不变。但每个节点安装好游戏的时间不一样。=ti+ci。总耗时就是max(ti+ci)

现在我们将问题简化一些。保留根节点u。将根节点下的子树，看成一个节点。对于ti和ci，我们可以这样看。假设遍历该节点需要的时间sz，一个该节点装好游戏的耗时d。则ti=sz+孩子节点的遍历次序，d=c。那么根据贪心的思想，我们会对等待时间最长（d-sz）的节点优先遍历。然后便是树形dp，由子节点推出父节点。

很明显

d[u] = max(d[u], d[son ] + 1 + T )，1表示u到该节点的耗时，T表示u到其他子节点又回来的耗时

若sz[i]表示遍历i相应的子树需要多少时间，d[i]表示i相应的子树全部都装好游戏的时间。

dp的状态转移：

d[u] = max(d[u], d[son] + 1 + sz[u]);
sz[u] += sz[son[i]] + 2; 2表示u->son->u

注意：1节点，只会在最后回来后才安装游戏。故d[1]初始化为0。其他节点初始化为c[i]，表示第一次来到就安装游戏。最终答案输出max(d[1], sz[1]+c[1])。此时d[1]表示1的所有子节点都安装好游戏的最小耗时，并且已经回到了1。sz[1]+c[1]表示1安装游戏的耗时。两者取最大便是答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <bits/stdc++.h>

#define pb push_back
#define db1(x) cout << #x << " = " << x << endl
#define db2(x, y) cout << #x << " = " << x << ", " << #y << " = " << y << endl
#define paging cout << "------------------" << endl
#define all(x) x.begin(), x.end()
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 5e5 + 10;
int n;
ll c[N];
ll d[N], sz[N];
vector<int> adj[N];
int son[N];
bool cmp(int a, int b) {
    return d[a] - sz[a] > d[b] - sz[b];
}
void dfs(int u = 1, int p = 0) {
    if(u != 1) d[u] = c[u];
    int cnt = 0;
    for (int v : adj[u]) if(v != p) dfs(v, u);
    for (int v : adj[u]) if(v != p) son[cnt++] = v;
    sort(son, son + cnt, cmp); // 只能在dfs之后sort。若在前面则会打乱son里的值。
    for (int i = 0; i < cnt; ++ i) {
        d[u] = max(d[u], d[son[i]] + 1 + sz[u]);
        sz[u] += sz[son[i]] + 2;
    }
}
void sol() {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++ i) scanf("%lld", &c[i]);
    for (int i = 1; i < n; ++ i) {
        int u, v; scanf("%d%d", &u, &v);
        adj[u].pb(v);
        adj[v].pb(u);
    }
    dfs();
    printf("%lld\n", max(d[1], sz[1] + c[1]));
}
int main() {
//    int _; scanf("%d", &_); while(_ --)
    sol();
    return 0;
}